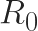determines whether a disease spreads over time
Restating the importance of knowing how long wild mosquitoes live
As I said in this post, we need to have better understanding of how long wild mosquitoes live. This would allow us to develop more accurate predictive models of the epidemiology of malaria, as well as other mosquito-borne diseases.
The predominant method used to estimate how long wild mosquitoes live is mark-release-recapture experiments (explained in this post.) These experiments are costly, both financially as well as in terms of time, and effort. Also, factors outside of the experimenter’s control, particularly weather, can cause wild variation in estimates of mosquito longevity. All of these issues with mark-release-recapture methods motivated the meta-analysis which I discussed previously.
Is there another way?
In 2009, a paper was published that showed that a type of spectroscopy, which measured the absorption of infrared light, could be used to predict adult mosquito age (Mayagaya et al., 2009). To estimate mosquito age, the authors started by shining infrared light through individual mosquitoes using an infrared spectroscopy machine like the one below.
Taken from Sikulu et al., (2011), Malaria Journal.
The authors used the above machine to measure how much light was absorbed, or reflected, across a range of wavelengths in the infrared part of the spectrum. Since the mosquitoes were reared in the lab, their age was known. As mosquitoes age there are changes in the mosquitoes’ chemical composition. Since different molecules absorb infrared light to differing degrees, the changes in the mosquitoes’ body chemistry causes differences in the spectra. However, these changes are subtle, meaning that the differences in the spectra are hard to see by eye. The difficulty in detecting these changes is made even harder due to the fact that there is quite a lot of inter-mosquito variation in spectra, as this next figure demonstrates.
The above figure shows a few examples of spectra drawn from a larger data base that we have compiled of the results of these experiments. In the figure there are 34 spectra. Each spectrum (coloured line) shows the result of an experiment on a single mosquito of known age. To try to identify patterns I have coloured each spectrum according to the age of the mosquito at the time of the experiment. For me, I find it difficult to see much of a pattern here. However, fortunately, there are methods that are more sensitive than my eyes!
Machine learning
Whilst it is difficult to visually detect any changes in spectra as mosquitoes age, statistical methods are more adept at these types of problem. In general, statistical methods are used when we want to isolate a ‘signal’ of interest, from a dataset that is noisy. This noise is due to the multitude of factors that can influence the result of an experiment, which are not of direct interest to the experimenter. In this case, as well as the changes in the spectra with age (the ‘signal’), the spectra also vary for a sample of mosquitoes of the same age. This unwanted variability (the ‘noise’) is due to differences in mosquito biochemistry, which are the result of different life histories, genetics, or experimental methods, for example. We would like whichever statistical method we choose to use to be able to see through this noise, and extract out the signal of interest. In this case, we want our statistical algorithm to be capable of estimating the age of individual mosquitoes from their noisy spectra, with a high degree of accuracy.
The experimenters chose to use a ‘Partial Least Squares’ algorithm for this task. This method works by trying to identify linear combinations of input (in this case, the spectra themselves) and output (age) variables, that are most highly correlated. I created the diagram below to try to graphically illustrate how this statistical method works.
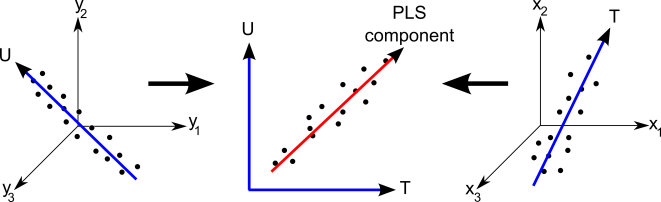
Whilst in this case there is only a single output variable, age, Partial Least Squares can be used to predict a range of output variables. Because of this, in the above figure I show a three dimensional output (the left hand plot), and three dimensional input (the right hand plot.) In our case there are 2,500 input variables, but this is hard to visualise, so in the above figure I just went for three variables. Here T and U illustrate the new variables that are created, from the input and output variables respectively. These variables are constructed so that their correlation with one another is as high as possible (illustrated in the middle plot.)
Results
The Mayagaya et al., (2009) authors calibrated a Partial Least Squares model using spectral data for over 250 observations of mosquito-age. This calibrated model was then used to estimate the age of a set of mosquitoes from their individual spectra. Importantly, these were different mosquitoes from those that were not used to calibrate the original model. Because these mosquitoes were not used to estimate the model, its performance on these ‘test’ set can be regarded as a fairly independent measure of its capability. The graph below shows the actual age versus the predicted for this test set.
Taken from Mayagaya et al., (2009), The American Journal of Tropical Medicine and Hygeine.
In the above figure each dot represents a mosquito at a particular age. The squares indicate average predictions for each of the real age groups. The points are arranged vertically because the mosquitoes were scanned at intervals of exactly three days: from an age of one day, to an age of nineteen days.
The results are quite extraordinary. It still amazes me how this indirect method is able to estimate the age of mosquitoes with any degree of accuracy. That it works at all is testament to the great efforts of the researchers involved.
Can we do better?
However, the predictions aren’t perfect. At younger ages there is a lot of variability. At higher ages, the predicted ages significantly understate the actual age. Are these results good enough for the original purpose of undertaking the research?
Remember, the original reason for undertaking this method was because knowledge about how long mosquitoes live in the wild is very important for understanding the epidemiology of mosquito-borne diseases. In the case of malaria, the impact of the disease on human populations is especially dependent on the age of mosquitoes. This is because mosquitoes must survive the extrinsic incubation period (see this page for a short explanation of this concept) to be able to transmit malaria. Whilst the length period depends on temperature, and possibly on mosquito species, a rough estimate of its duration is 9-12 days. So mosquitoes need to live at least this long to be able to transmit malaria. In reality they will need to be older, since they first have to find a mate, then subsequently bite an infected human. Therefore, perhaps it is more realistic to suppose that mosquitoes must live for at least 10-13 days in order to be able to pass on the disease. Thus, whether malaria spreads through a region, or dies out, depends crucially on the age-structure of the population, particularly whether enough mosquitoes live longer than about 10 days.
The results above indicate reasonable predictive capability for younger mosquitoes, however they also demonstrate that the method falls down for older specimens. However, from the previous discussion, it is precisely these mosquitoes whose age we need to determine! If there are a lot of very old mosquitoes (20 days plus, for example) in a particular region, then malaria will spread much more easily. This also highlights why insecticide-treated bed nets, and other methods that aim to suppress adult mosquito populations, are so effective: they reduce the number of mosquitoes that live long enough to transmit malaria.
So, we need to do a bit better. The research of the authors is a good start, but we need to build on their success.
Our approach
Thomas Churcher at Imperial and I, together with our research collaborators Maggy Sikulu, and Floyd Dowell, have been working towards improving the use of this technology. We started by amassing a data base, of over 5,000 individual spectra. Each of these spectra corresponds to a particular mosquito sample, whose age is known. The data come from a variety of sources, at a range of different laboratories. By using this data we aim to build a statistical model that is robust to variation in experimental technique, as well as geographic variation in mosquitoes.
We have used cutting-edge machine learning techniques, to build a tool that can accurately predict individual mosquito age. The results of this research are promising. The below figure illustrates the predictions made by our machine learning algorithm across approximately 1,000 independent mosquito samples.
In the above figure, the black dots represent individual samples, and the orange line shows the optimal case (actual=predicted). The dark blue line (mostly obscured by the orange) represents our average model prediction at each value of mosquito age, and the blue shading indicates 95% predictive intervals for our algorithm.
These results illustrate that we have removed many of the undesirable features from the results of the original paper: there is reasonable prediction of mosquito age across the entire range that we surveyed. The average predictive error is about 2.5 days. This means that about 70% of our predictions lie within the interval: 
We’re pretty pleased with these results and are currently in the midst of finishing our paper for submission. Along with the above results, in the paper we demonstrate that the use of our algorithm could be used to infer demographic parameters for mosquito populations. All in all it’s quite exciting. After the paper is (hopefully) accepted, I will post more of the results here.
